| |
|
|
| Calculer l'aire d'une sphère |
|
|
|
|
|
Indiquez la mesure du rayon pour avoir l'aire de la sphère.
|
|
| Comment calculer l'aire d'une sphère |
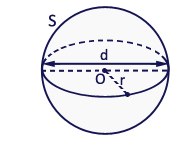
L'aire d'une sphère est égale au carré du rayon multiplié par π et par 4. (π vaut environ 3,14).
Aire d'une sphère = 4π x (Rayon)²
Aire d'une sphère = 4πr²
Exemple :
Soit une sphère S de rayon r = 3 cm, on utilise π = 3,14
L'aire de la sphère S = 4 x 3,14 x (3 cm)²
L'aire de la sphère S = 113,04 cm²
Remarque :
Toutes les mesures doivent être exprimées dans la même unité.
|
|
| Quelques propriétés de la sphère |
|
Une sphère de centre O et de rayon r est l'ensemble des points M de l'espace tels que OM = r.
Le rayon de la sphère est un segment délimité par le centre et un point quelconque de la sphère.
La longueur du rayon est la distance entre un point de la sphère et le centre.
Le diamètre est un segment de droite passant par le centre et délimité par deux points de la sphère.
La longueur du diamètre est égale à deux fois la longueur du rayon.
Toute droite passant par le centre d'une sphère coupe celle-ci en deux points diamétralement opposés.
La sphère peut être engendrée par un demi-cercle tournant autour d'un axe : la sphère est donc une surface de révolution.
|
|
| Suggestions d'articles : |
|
|
|
